Robotic Manipulators
Exercise List

Spatial Representation
Exercise 1
How many degrees of freedom are needed to represent a rigid body in the plane?

Spatial Representation
Exercise 2
Is a robot with rigid links a rigid body? Justify.

Spatial Representation
Exercise 3
Consider a rigid body moving in space. Let \(A\) and \(B\) be two particles of the body, and \(p^A_0(t), p^B_0(t)\) be their positions over time relative to a fixed frame \(\mathcal{F}_0\). Can we assert that \(\frac{d}{dt} \|p^A_0(t)-p^B_0(t)\| = 0\) for all \(t\)? Justify.

Spatial Representation
Exercise 4
Consider three independent rigid bodies moving in three-dimensional space. What is the minimum amount of information needed to track the position of all of the system’s particles over time?

Spatial Representation
Exercise 5
Show that the inverse of the HTM:
$$H = \left(\begin{array}{cc} Q & s \\ 0_{1 \times 3} & 1 \end{array}\right)$$is the following HTM:
$$H^{-1} = \left(\begin{array}{cc} Q^T & -Q^Ts \\ 0_{1 \times 3} & 1 \end{array}\right).$$

Spatial Representation
Exercise 6
Consider the following image, in which a camera and a six-sided die are placed in some yet unknown arrangement on a table. Also consider that the distance unit (u.d.) used to describe the translation is roughly as shown in the figure below.
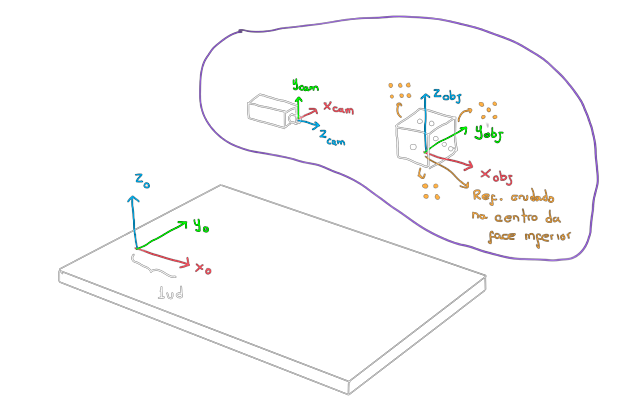
Spatial Representation
Exercise 6
Suppose we have the HTMs from reference \(\mathcal{F}_0\) to the camera, and from the object to the camera:
$$H_0^{cam} = \LARGE{\Bigg(}\begin{array}{cccc} 0 & 1 & 0 & 3 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & -1 & 3 \\ 0 & 0 & 0 & 1 \end{array}\LARGE{} , \quad H_{obj}^{cam} = \LARGE{\Bigg(}\begin{array}{cccc} 0 & 0 & 1 & -3 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\LARGE{}.$$(a) Compute the transformation from \(\mathcal{F}_0\) to the die, \(H_0^{obj}\).
(b) Sketch how the camera and the die appear in the diagram.

Spatial Representation
Exercise 7
Consider the image to the side, showing the movement of the earth around the sun. It is composed of two motions: a rotation around the sun at angular frequency \(\omega_A\) and a rotation around itself (around its own \(z\) axis) at angular frequency \(\omega_D\). \(d_S\) is the distance from the center of the sun to the center of the earth.
Compute the HTM from the sun’s reference, \(\mathcal{F}_0\), to the earth’s reference \(\mathcal{F}_T\), in terms of the parameters \(\omega_A, \omega_D, d_S\) and time \(t\). Assume that at \(t=0\), both \(x\)-axes are aligned.
Caution: the final rotational speed of the earth around itself must be exactly \(\omega_D\). Check if that is the case after building the HTM.
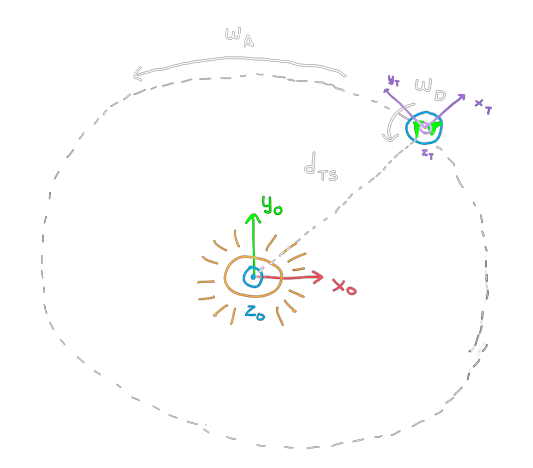
Spatial Representation
Exercise 8
Let \(A\) be a skew-symmetric matrix (\(A^T = -A\)), and let \(\epsilon\) be a number so small that \(\epsilon^2 = 0\). Can we say that \(Q = I_{3 \times 3} + \epsilon A\) is a rotation matrix? Justify.

Spatial Representation
Exercise 9
Let \(Q_1\) and \(Q_2\) be rotation matrices around the same axis.
(a) Can we state that \(Q_1Q_2 = Q_2Q_1\)? Justify.
(b) How do we interpret the rotation \(Q_1Q_2\) (with respect to the original \(Q_1\) and \(Q_2\))?

Spatial Representation
Exercise 10
Can we assert that for every rotation matrix \(Q\) there exists a nonzero vector \(r\) such that \(Qr = r\)? Justify.

Spatial Representation
Exercise 11
Consider the following image, in which a park ride rotates in two distinct axes, \(z_0\) and \(z_1\), with constant speeds \(\omega_0\) and \(\omega_1\), respectively. The \(z_0\) axis is fixed and the \(z_1\) axis is mobile.
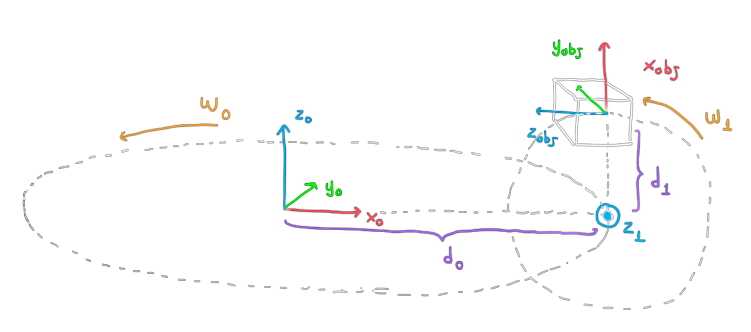
Spatial Representation
Exercise 11
Compute the HTM from reference \(\mathcal{F}_0\) to the object’s reference, in terms of the parameters (\(\omega_0, d_0, \omega_1, d_1\)) and time \(t\).
Assume that at \(t=0\), the \(x\)-axes of both references are aligned.

Spatial Representation
Exercise 12
Consider two references \(\mathcal{F}_A\) and \(\mathcal{F}_B\), with the transformation \(T_A^B\) between them.
Consider a point \(P\) whose description in \(\mathcal{F}_B\) is the column vector \(p_B\). How can we find its description \(p_A\) in \(\mathcal{F}_A\)?

Spatial Representation
Exercise 13
Consider a rigid body moving in space. The HTM from a fixed reference \(\mathcal{F}_0\) to the object’s reference is \(H_0^{obj}(t) = R_z(2t)D_x(1)R_x(\pi/2)\).
Consider a particle \(P\) in the object whose coordinates in the object’s reference are (constant) \(p^P_{obj} = (0 \ 1 \ 0)^T\). Compute the coordinates of the particle in reference \(\mathcal{F}_0\) at time \(t\): \(p^P_0(t)\).

Spatial Representation
Exercise 14
Consider a drone with a manipulator mounted on it. There is a reference \(\mathcal{F}_d\) attached to the drone, a reference \(\mathcal{F}_e\) attached to the manipulator’s end-effector, and a fixed reference \(\mathcal{F}_0\).
Knowing that at a certain instant of time \(T_0^e = R_z(30^o)D_x(2m)\) and \(T_d^e = R_y(90^o)D_z(1m)\), what would be the value of the transformation \(T_d^0\) between the drone and the fixed reference?
