Robotic Manipulators
Answers

Spatial Representation
Exercise 1 - Answer
Three degrees of freedom are required, 2 for the displacement in the plane and 1 for the rotation in the plane.

Spatial Representation
Exercise 2 - Answer
No! The robot as a whole is not a rigid body. Take two particles in different links. Then, depending on the movement of the robot, the distance between them can increase or decrease, proving that it is not a rigid body.

Spatial Representation
Exercise 3 - Answer
Yes. After all, \(\|p_0^A(t)-p_0^B(t)\|\) is the distance between the two particles \(A\) and \(B\) at time \(t\). By definition, in a rigid body, this quantity is constant for all \(t\), and therefore the time derivative is 0.

Spatial Representation
Exercise 4 - Answer
18. Each rigid body requires 6 numbers, at a minimum (e.g., three numbers for the position of the reference center and 3 Euler angles). Since the bodies are independent, there are 6 numbers for each of the three bodies.

Spatial Representation
Exercise 5 - Answer
To show that one matrix \(G\) is the inverse of the other, just show that \(HG = GH = I_{4 \times 4}\). It is not difficult to show this if we use block-by-block matrix multiplication and the fact that \(Q^TQ=QQ^T=I_{3 \times 3}\) when \(Q\) is an identity matrix.

Spatial Representation
Exercise 6 - Answer
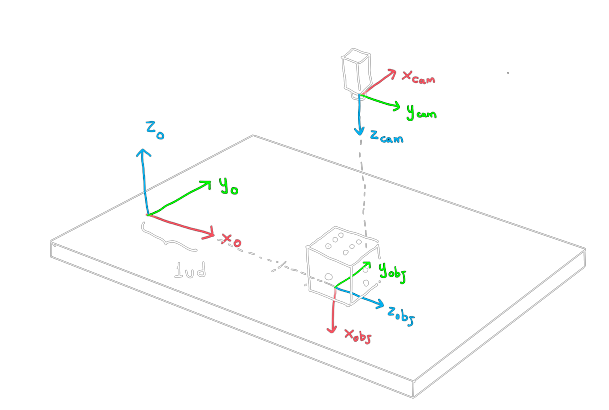
Note that \(H_0^{obj} = H_0^{cam}H_{cam}^{obj}\). The matrix \(H_{cam}^{obj}\) was not given, but note that \(H_{cam}^{obj} = (H_{obj}^{cam})^{-1}\). Using the property to calculate the inverse of HTMs seen in the previous example and doing the math, we have:
$$H_0^{obj} = \LARGE{\Bigg(}\normalsize{}\begin{array}{cccc} 0 & 0 & 1 & 3 \\ 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array}\LARGE{\Bigg)}\normalsize{}$$Just read this reference frame in the reference frame \(\mathcal{F}_0\) and we will know how the data is...
Continues on the next slide...
Spatial Representation
Exercise 6 - Answer
Spatial Representation
Exercise 7 - Answer
We have the HTM:
$$H_0^{T}(t) = R_z(\omega_At)D_x(d_{TS})R_z((\omega_D-\omega_A)t).$$It may seem curious that the left multiplication is \(R_z((\omega_D-\omega_A)t)\), and not of \(R_z(\omega_Dt)\). It turns out that, if we do it this way, the resulting rotation matrix of the HTM will be a rotation in \(z\) of an angle \((\omega_A+\omega_D)t\). This implies that the angular velocity of the Earth's rotation around itself is \(\omega_A+\omega_D\), which is not what was specified.

Spatial Representation
Exercise 8 - Answer
Yes. For this, we need to have \(Q^TQ = QQ^T = I_{3 \times 3}\) and \(\det(Q)=+1\).
Note that \(Q^T = I_{3 \times 3}-\epsilon A\) (we used the antisymmetry property of \(A\) and the linearity of transposition). So \(Q^TQ = I_{3 \times 3} -\epsilon A + \epsilon A - \epsilon^2 A^2\). Since we consider \(\epsilon^2 = 0\), we have \(Q^TQ = I_{3 \times 3}\). Similarly, we can prove that \(QQ^T = I_{3 \times 3}\).
To show \(\det(Q)=+1\), you can write the matrix \(I_{3 \times 3}+\epsilon A\) with a generic antisymmetric matrix \(A\) and calculate the determinant. By setting \(\epsilon^2 = 0\), you will see that it has a determinant of +1.
Note: This (apparently) innocent result is linked to a much deeper theory, called Lie Theory, and illustrates an important property of the geometry of the rotation space.

Spatial Representation
Exercise 9 - Answer
(a): Yes. Rotations on the same axis commute.
(b): If \(Q_1\) is a rotation of an angle \(\theta_1\) on an axis \(r\) and \(Q_2\) a rotation of an angle \(\theta_2\) on the same axis, \(Q_1Q_2 = Q_2Q_1\) is a rotation on the axis \(r\) of an angle \(\theta_1+\theta_2\).

Spatial Representation
Exercise 10 - Answer
Yes. Every rotation is a rotation on an axis. Let \(r\) be a non-zero vector that is on the rotation axis of the matrix \(Q\). Then \(r' = Qr\) represents the point \(r\) rotated on this axis. But since the point is on the axis, nothing will happen, and therefore \(r' = r = Qr\).
Example: rotating the vector \(r = (0 \ 0 \ 1)^T\) on the \(z\) axis does not change it.

Spatial Representation
Exercise 11 - Answer
The answer is:
$$R_z(\omega_0t) D_x(d_0)R_y(-\omega_1t)D_x(d_1).$$
Spatial Representation
Exercise 12 - Answer
Sejam \(Q_A^B\) e \(s_A^B\) a matriz de rotacao e vetor de deslocamento extraido de \(T_A^B\)
Entao \(p_A = Q_A^B p_B + s_A^B\). Ou seja, para fazermos a mudança de coordenada de um vetor de um referencial \(\mathcal{F}_B\) para \(\mathcal{F}_A\), aplicamos a transformação rigida de \(\mathcal{F}_A\) para \(\mathcal{F}_B\) ao ponto escrito em \(p_B\)!

Spatial Representation
Exercise 13 - Answer
Este problema é um caso particular do problema de transformação de referenciais explicado aqui.
A lógica e a seguinte: considere um terceiro referencial \(\mathcal{F}_C\) cujo centro seja esse ponto \(P\) (a orientação dele é irrelevante aqui). Seja \(T_B^C\) a matriz de transformação entre \(\mathcal{F}_B\) e \(\mathcal{F}_C\). Entao sabemos, devido as duas interpretacões de MTHs, que \(T_B^C\) é o referencial \(\mathcal{F}_C\) escrito em \(\mathcal{F}_B\). Devido a isso, sabemos que a parte de translação de \(T_B^C\) é precisamente \(p_B\).
Por exatamente a mesma logica, seja \(T_A^C\) a transformacao entre \(\mathcal{F}_A\) e \(\mathcal{F}_C\). A parte de translação dessa matriz é precisamente \(p_A\).
Mas, sabemos que \(T_A^C = T_A^B T_B^C\). Se lermos so a parte de translacão dessa equação, chegamos no resultado desejado.

Spatial Representation
Exercise 13 - Answer
Calculando a MTH resultante, podemos extrair a rotação e a translação:
$$s(t) = \LARGE{\Bigg(}\normalsize{}\begin{array}{c} \cos(2t) \\ \sin(2t) \\ 0 \end{array}\LARGE{\Bigg)}\normalsize{} \ , \ Q(t) = \LARGE{\Bigg(}\normalsize{}\begin{array}{ccc} \cos(2t) & 0 & \sin(2t) \\ \sin(2t) & 0 & -\cos(2t) \\ 0 & 1 & 0 \end{array}\LARGE{\Bigg)}\normalsize{}$$Então temos que:
$$p^P_0(t) = Q(t)p^P_{obj}+s(t) = \LARGE{\Bigg(}\normalsize{}\begin{array}{c} \cos(2t) \\ \sin(2t) \\ 1 \end{array}\LARGE{\Bigg)}\normalsize{}.$$
Spatial Representation
Exercise 14 - Answer
Sabemos que \(T_0^e = T_0^d T_d^e\). Então \(T_0^d = T_0^e (T_d^e)^{-1}\). Usando a fórmula da inversa desta questão, obtemos:
$$T_0^d = \underbrace{\normalsize{\Bigg(}\tiny{}\begin{array}{cccc} \frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 & \sqrt{3} \\ \frac{1}{2} & \frac{\sqrt{3}}{2} & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\normalsize{\Bigg)}}_{T_0^e} \underbrace{\normalsize{\Bigg(}\tiny{}\begin{array}{cccc} 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & -1 \\ 0 & 0 & 0 & 1 \end{array}\normalsize{\Bigg)}\tiny{}}_{(T_d^e)^{-1}} = \normalsize{\Bigg(}\tiny{}\begin{array}{cccc} 0 & -\frac{1}{2} & -\frac{\sqrt{3}}{2} & \sqrt{3} \\ 0 & \frac{\sqrt{3}}{2} & -\frac{1}{2} & 1 \\ 1 & 0 & 0 & -1 \\ 0 & 0 & 0 & 1 \end{array}\normalsize{\Bigg)}\tiny{}. $$Mas queremos \(T_d^0\), não \(T_0^d\). Mas \(T_d^0=(T_0^d)^{-1}\). Então:
$$T_d^0 = \normalsize{\Bigg(}\tiny{}\begin{array}{cccc} 0 & 0 & 1 & 1 \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} & 0 & 0 \\ -\frac{\sqrt{3}}{2} & -\frac{1}{2} & 0 & 2 \\ 0 & 0 & 0 & 1 \end{array}\normalsize{\Bigg)}\tiny{}. $$