Robotic Manipulators
Exercise List

Forward Kinematics
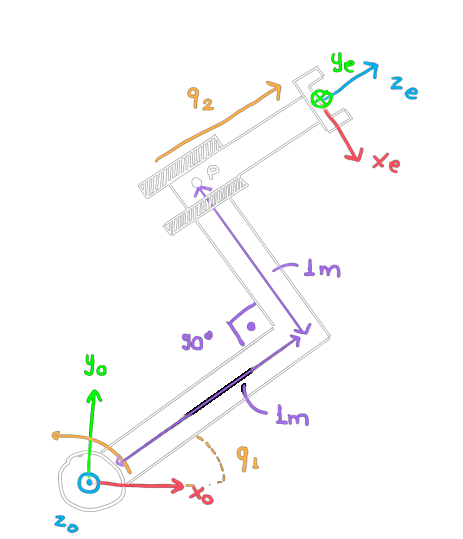
Exercise 1
Consider the robot on the side, with one rotational joint and one prismatic joint.
Consider that when \(q_1=0\) the \(z_e\) axis is aligned with \(x_0\).
Consider that when \(q_2=0\) the center of the reference frame \(\mathcal{F}_e\) is at point \(P\).
The drawing shows the positive direction of rotation/translation of the two joints.
Calculate its forward kinematics for the end-effector, i.e., the HTM \(H_0^{e}(q)\).
Forward Kinematics
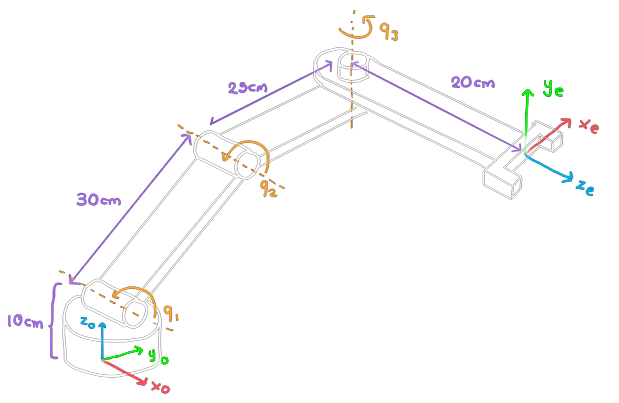
Exercise 2
Consider the manipulator below, with three rotational joints.
Forward Kinematics
Exercise 2
Consider that the \(x_0\) axis is aligned with the line of the first joint, and that a displacement in \(z_0\) makes the center of the reference frame \(\mathcal{F}_0\) go to this line.
Also consider that the lines of the first two joints are parallel, and that the second and third lines are orthogonal.
(a) Create the four Denavit-Hartenberg reference frames.
(b) Derive the \(3 \times 4 = 12\) parameters.
(c) Using these reference frames, calculate the forward kinematics from the reference frame \(\mathcal{F}_0\) to the end-effector reference frame, \(\mathcal{F}_e\).

Forward Kinematics
Exercise 3
Does a Denavit-Hartenberg reference frame necessarily have to have its center within the link it is attached to? Justify.

Forward Kinematics
Exercise 4
Can we have two distinct Denavit-Hartenberg reference frames for the same robot that have the same center? Justify.

Forward Kinematics
Exercise 5
We know that a transformation between two generic reference frames requires at least 6 numbers.
Knowing this, explain why the transformation between two Denavit-Hartenberg reference frames requires fewer parameters (in this case, 4).

Forward Kinematics
Exercise 6
Can we always guarantee that the inverse kinematics problem has a solution? Justify.

Forward Kinematics
Exercise 7
Consider the scenario on the side, which can be created by the following code in UAIBot:
import uaibot as ub
import numpy as np
#Create the scenario
robot = ub.Robot.create_abb_crb(ub.Utils.trn([0,0,0.2]))
texture_table = ub.Texture(
url='https://raw.githubusercontent.com/viniciusmgn/uaibot_content/master/contents/Textures/rough_metal.jpg',
wrap_s='RepeatWrapping', wrap_t='RepeatWrapping', repeat=[1, 1])
material_table = ub.MeshMaterial(texture_map=texture_table, roughness=1, metalness=1, opacity=1)
table1 = ub.Box(name="table1", htm = ub.Utils.trn([0.8,0,0.15]), width=0.5, depth=0.5, height=0.4, mesh_material=material_table)
table2 = ub.Box(name="table2", htm = ub.Utils.trn([0,-0.8,0.15]), width=0.5, depth=0.5, height=0.4, mesh_material=material_table)
table3 = ub.Box(name="table3", htm = ub.Utils.trn([0,0,0.1]), width=0.3, depth=0.3, height=0.2, mesh_material=material_table)
obstacle = ub.Box(name="obstacle", htm = ub.Utils.trn([0.8,-0.8,0.5]), width=0.6, depth=0.6, height=1, mesh_material=material_table)
material_cube = ub.MeshMaterial(roughness=1, metalness=1, opacity=1, color="purple")
cube = ub.Box(name="cube", htm = ub.Utils.trn([0.8,0,0.4]), width=0.1, depth=0.1, height=0.1, mesh_material=material_cube)
sim = ub.Simulation.create_sim_factory([robot, table1, table2, table3, obstacle, cube])
Forward Kinematics
Exercise 7
Create a code in UAIBot for the robot to pick up the purple block on one table and place it on the other, without hitting the obstacles. The robot should pick up and place the object from above!
Use inverse kinematics and linear interpolation, as in this example from Class 3.
Use the function robot.attach_object(cube) to make the end-effector grab the object when it is in the correct pose.
The function ikm accepts a parameter q0, trying to find a configuration in inverse kinematics close to q0. Use this to your advantage.