Robotic Manipulators
Exercise List

Differential Kinematics
Exercise 1
Let \(Q(t)\) be a rotation matrix parameterized in time and differentiable.
Can we assert that \(\det(\dot{Q}(t)) = 0\) for all \(t\)? Justify.

Differential Kinematics
Exercise 2
Suppose a body with non-zero linear and angular velocities \(v(t), \omega(t)\) for all \(t\).
Also assume that \(v(t)\) and \(\omega(t)\) are parallel vectors for all \(t\).
Can we assert that, in this situation, for all times \(t\), there will exist at least one particle \(P\) in the body with zero velocity (measured with respect to the reference frame \(\mathcal{F}_0\))? Justify.

Differential Kinematics
Exercise 3
Consider a moving reference frame \(\mathcal{F}_{m}\). Let \(z(t)\) and \(\omega(t)\) be the \(z\) axis of its reference frame and its angular velocity, both written with respect to a fixed reference frame \(\mathcal{F}_0\).
Can we assert that \(\frac{d}{dt}z(t)\) and \(\omega(t)\) are orthogonal vectors? Justify.

Differential Kinematics
Exercise 4
Let \(A\) be a generic \(3 \times 3\) skew-symmetric matrix.
Can we assert that there always exists a three-dimensional vector \(a\) such that \(S(a)=A\)? Justify.

Differential Kinematics
Exercise 5
Can we assert that for every three-dimensional vector \(a\), there exists a non-zero vector \(b\) such that \(S(a)b=0_{3 \times 1}\)? Justify.

Differential Kinematics
Exercise 6
Consider a rigid body. Let \(P\) be the center of the reference frame \(\mathcal{F}_{obj}\) attached to the object.
Let \(R\) be the radius of the smallest sphere centered at \(P\) that encompasses the entire object. Note that this value of \(R\) will be constant.
Prove that the scalar velocity of any particle at time \(t\) cannot exceed \(\|v(t)\|+R\|\omega(t)\|\), where \(v(t)\) and \(\omega(t)\) are the linear and angular velocity vectors of the object (with respect to the reference frame \(\mathcal{F}_{obj}\)).

Differential Kinematics
Exercise 7
(a) Calculate the linear and angular velocity vectors of the earth (with respect to the reference frame attached to its center and measured in the reference frame \(\mathcal{F}_0\)) from the Exercise 7 of Spatial Representation.
(b) Calculate the linear and angular velocity vectors of the toy (with respect to the reference frame attached to its center and measured in the reference frame \(\mathcal{F}_0\)) from the Exercise 11 of Spatial Representation.
Note that the calculations will be in terms of the respective parameters and time \(t\).

Differential Kinematics
Exercise 8
Calculate the Geometric Jacobian for the robot on the side, from Exercise 1 of Forward Kinematics.
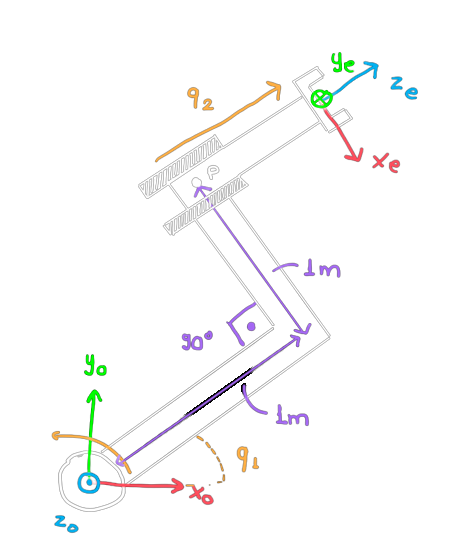
Differential Kinematics
Exercise 9
Calculate the Geometric Jacobian for the robot on the side, from Exercise 2 of Forward Kinematics.
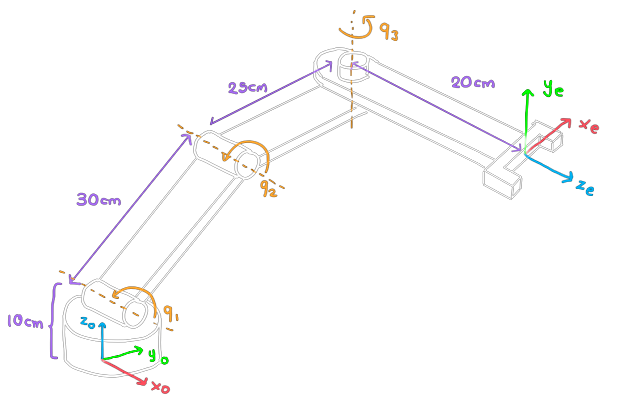
Differential Kinematics
Exercise 10
Can we assert that in a robot with only linear joints the matrix \(J_\omega(q)\) is zero? Justify.

Differential Kinematics
Exercise 11
The vector angular acceleration \(\alpha\) is the time derivative of the angular velocity vector, \(\alpha = \dot{\omega}\).
That said, can we assert that, at a given instant of time \(t\), the robot's end-effector can have non-zero angular acceleration \(\alpha(t)\) while having zero joint acceleration \(\ddot{q}(t)\)? Justify.

Differential Kinematics
Exercise 12
Let \(\xi_{d1}, \xi_{d2} \in \mathbb{R}^6\) be desired velocities for the end-effector. Suppose that in a given configuration \(q\) it is possible to find joint velocities \(\dot{q}_1\) and \(\dot{q}_2\) that achieve these velocities, respectively.
Can we then assert that, for this same configuration \(q\), there exists a joint velocity \(\dot{q}_3\) that achieves the velocity \(\xi_{d3} = \xi_{d1}+\xi_{d2}\)? Justify.

Differential Kinematics
Exercise 13
(a) Use the UAIBot to find out if the configuration
$$q = (0 \ \ 1{,}57 \ \ 0{,}1 \ \ 0{,}1 \ \ 0{,}1 \ \ 0)^T \ rad$$of the robot Staubli TX60 is singular (use the function Robot.create_staubli_tx60 to create it).
Use the function numpy.linalg.eig from Numpy, which calculates eigenvalues, to calculate the singular values. Consider a singular value as zero if it is less than \(10^{-5}\).
(b) If it is not singular, use the UAIBot to find out what the joint velocity should be in this configuration to make the end-effector have a velocity of 1m/s in \(z_0\) and all other velocity components 0.

Differential Kinematics
Exercise 14
(a) Use the UAIBot to calculate the velocity \(\xi\) of the end-effector in the initial configuration of the robot Epson T6 when only the first joint rotates at a speed of 1 rad/s (use the function Robot.create_epson_t6 to create it).
(b) Check if the result makes sense.

Differential Kinematics
Exercise 15
A common mistake for beginners in robotics is the following: let \(\phi(t) = (\gamma(t) \ \beta(t) \ \alpha(t))^T \in \mathbb{R}^{3 \times 1}\) be the Euler angles of the moving end-effector (angles x, y, and z, respectively). Then, it is common to think that \(\frac{d}{dt}\phi(t) = \omega(t)\).
This is not true, in general (only in very specific cases)! Show this using the UAIBot.
Make a robot perform some joint movement. Calculate \(\omega(t)\) and \(\frac{d}{dt}\phi(t)\) (use the function Utils.euler_angles). Show that eventually they will be different.
